|

|
T.L. (Thomas) Harrewijn
In het begin van de twintigste eeuw zijn de eerste gewapend betonnen bruggen in Nederland gebouwd. Het overgrote deel van de huidige infrastructuur is vóór 1985 gebouwd. De eerste ontwerpnorm voor gewapend beton in Nederland is opgenomen in de ‘Gewapend betonvoorschriften’ uit 1912 [1]. Deze norm is ongeveer iedere tien jaar herzien met nieuw vergaarde kennis in mechanica, materiaaleigenschappen en praktische ervaring. Het toenmalige Ministerie van Infrastructuur & Waterstaat publiceerde de eerste ontwerpnorm voor stalen bruggen in 1933 genaamd: ‘Voorschriften voor het ontwerp van Stalen Bruggen’ (VOSB1933) [2] die tevens belastingmodellen voor verkeer beschreef.
In de VOSB worden bruggen gecategoriseerd, gebaseerd op (verwachte) type belasting op de brug. Bruggen voor normaal verkeer zijn gecategoriseerd met een verkeersklasse afhankelijk van de functie in het wegennetwerk, zie Tabel 1. In het begin van de jaren ’60, is de VOSB1963 geïntroduceerd waarin de classificering en notering van de verkeersklassen zijn gewijzigd. Aanhoudende toename van verkeersintensiteiten en (gemiddelde) aslasten
heeft de belastingmodellen verder doen ontwikkelen. Het huidig belastingsmodel (BM1) volgens de NEN-EN 1991-2 [3] maakt geen onderscheid tussen verschillende categorieën van wegen in vergelijking tot de oude normen. In Nederland is daarom een belastingmodel voor bruggen in het beheer van decentrale overheden opgesteld [4].
Bruggen met
• een maximale overspanning van 20 m,
• maximaal 125.000 aantal passages van zware voertuigen per rijstrook, en
• een ligging in een route waar verkeer met jaarontheffingen voor zware transporten niet is toegestaan,
komen hiervoor in aanmerking.
Aan de ander kant heeft de ontwikkeling van de ontwerpnormen de materiaaleigenschappen en de methoden voor het bepalen van capaciteiten doen veranderen. De voornaamste veranderingen in verscheidene methoden in het brugontwerp zijn:
• de berekening van de stootfactor,
• de bepaling van de spreidingsbreedte (effectieve breedte),
• de methoden voor het bepalen van doorsnedecapaciteiten (N-methode vs. breukmethode) en
• het gebruik van glad staal vs. geribd staal, wat de scheurwijdtecriteria heeft geïntroduceerd.
Tabel 1. Verkeersklasse voor verkeer, met de classificatie volgens de VOSB1933 en de VOSB1963, waar een lagere verkeersklasse dan 30 is weggelaten.
|
VOSB1933
[verkeersklasse]
|
VOSB1963
[verkeersklasse]
|
Brug
|
|
A
|
60
|
in het hoofdverkeerswegen
|
|
B
|
45
|
in het hoofdverkeerswegen met incidenteel zwaar verkeer
|
|
C
|
30
|
niet bestemd voor zwaar verkeer
|
|
D
|
-
|
voor licht verkeer (voetgangers)
|
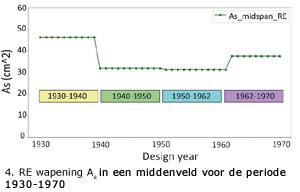
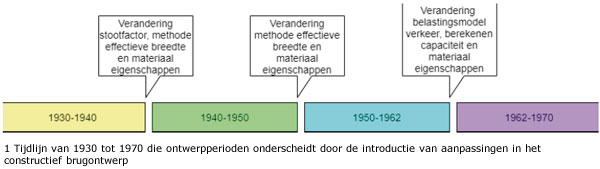
Vier tijdsperioden van constant brugontwerp aan zowel de capaciteits- als de belastingskant in de periode 1930 - 1970 zijn te onderscheiden. In figuur 1 is de periode 1930-1970 opgedeeld door de introductie van ontwerpwijzigingen. Zodoende is het stichtingsjaar de indicator voor de toegepaste ontwerpmethode. Uit een onderzoek naar gemeentelijke bruggen [5] blijkt dat de archivering van bestaande bruggen vaak incompleet of
zelfs onbekend is. Deze bruggen bevinden zich veelal in een lokaal wegennetwerk en zijn zodoende (vaak) ontworpen in betonsterkteklasse B45. Door de verandering van de belastingsmodellen, de capaciteitsbepaling, de restlevensduur en het gebrek aan informatie over deze bruggen, is er bezorgdheid over de capaciteitsmarge van deze bruggen.
De huidige methode om wapening te herleiden bij verloren documentatie, is door de staafdiameter en staafafstand te meten m.b.v. X-Ray scannen. Echter, deze methode is niet exact genoeg, veroorzaakt verkeershinder en kost dus geld en tijd. Dit afstudeeronderzoek stelt Reverse Engineering (RE) voor als alternatief om op afstand de bestaande constructie te kunnen beoordelen. In het proces van RE van de bestaande brug is het (correcte) origineel constructief ontwerp gereproduceerd, wat resulteert in de originele krachtswerking met bijbehorende minimale capaciteit. Vanuit deze minimale RE buigend momentcapaciteit, is de wapeningslayout voor wat betreft de staafdiameter en staafafstand verondersteld.
REVERSE ENGINEERING TOOL - AUTOMATISEREN VAN HET RE-PROCES
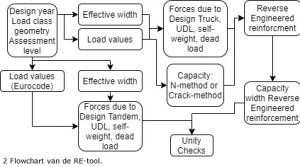
De RE-tool is gecodeerd in de programmeertaal Python [6] om de dimensionering van de benodigde wapening volgens de oude ontwerpnormen te bepalen. Figuur 2 geeft met een flowchart de stappen weer die de tool doorloopt.
De tool gebruikt het stichtingsjaar, de verkeersklasse en de geometrie van de brug als inputparameters. De gebruiker kan mogelijke staafdiameters aangeven waaruit de tool mag kiezen voor het RE van de mogelijke wapening lay-out. De RE-wapening is per meter plaatbreedte bepaald en dus in breedterichting constant verondersteld. De verkeersbelasting vanuit de specifieke verkeerklasse, het eigen gewicht en de rustende belasting resulteren in de
maatgevende doorsnedekrachten waarvoor de wapening ontworpen is. Het onderzoek heeft zich beperkt tot de hoofdwapening in het veldmidden van een overspanning en op die bij de tussensteunpunten. Het valideren van de tool is uitgevoerd met de originele wapeningstekeningen van bestaande bruggen, gebouwd in de periode 1930-1970. Tabel 2 toont de RE-wapening, de hoeveelheid wapening van de tekening en de nauwkeurigheid van de computer code vergeleken met de wapeningstekening. Gemiddeld wordt er 10% minder wapening berekend door de tool dan dat er op de originele wapeningstekeningen staat. Dit laat een conservatieve methode zien die de capaciteit van de bestaande brug niet overschat.
TOETSEN VAN DE RE-BRUGGEN
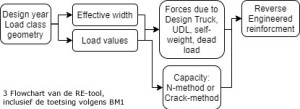
Vervolgens kan de RE-brug worden beoordeeld met BM1 en de beoordelingsnormen (NEN8700 [7] /NEN8701 [8], RBK- 1-1 [9]) gebaseerd op de Eurocode. Toetsen op buigend moment en dwarskracht voor het bestaand brugontwerp met RE wapening zijn uitgevoerd. Dit is uitgevoerd door REtool uit te breiden met deze toetsen, zie de uitbreiding van figuur 2 naar figuur 3. De capaciteitmarges van de herberekende bruggen zijn getoetst volgens de herberekeningsnormen. Het gangbare bi-lineaire spanningsdiagram van gewapend beton is toegepast voor de massieve doorsnede voor het bepalen van de buigend momentcapaciteiten. De dwarskrachtcapaciteit is bepaald volgens de Eurocode en de RBK v1.1[9] via de formules 6.2a en 6.2b. BM1 uit de Eurocode is toegepast met belastingsfactoren volgens de NEN8700 (verbouwniveau) [7] en het belastingsmodel voor decentrale overheden [4]. De spreiding van de lastmodellen is bepaald met de methode van Guyon- Massonnet [10].
| Brug |
RE
[cm2/m] |
Tekening
[cm2/m] |
Nauwkeurigheid
[%] |
A
|
Middenveld |
52 |
57 |
91 |
| Middensteunpunt |
71 |
73 |
97 |
| B |
Middenveld |
28 |
27 |
104 |
| Middensteunpunt |
26 |
31 |
84 |
| C |
Middenveld |
43 |
53 |
81 |
| Middensteunpunt |
50 |
53 |
94 |
| D |
Middenveld |
46 |
49 |
94 |
| Middensteunpunt |
46 |
49 |
94 |
| E |
Middenveld |
44 |
49 |
90 |
| Middensteunpunt |
44 |
49 |
90 |
| F |
Middenveld |
33 |
37 |
89 |
| Middensteunpunt |
40 |
56 |
71 |
Tabel 2 RE-wapening door de computer code vs. originele documentatie.
PARAMETRISCHE STUDIE
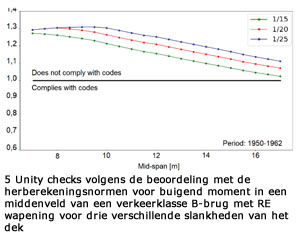
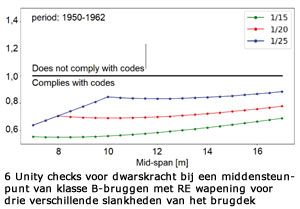
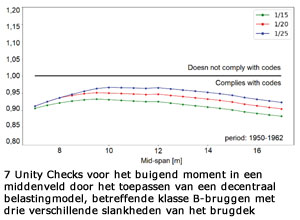
De tweede toepassing van de tool is het uitvoeren van een parametrische studie om het constructief ontwerp van bestaande bruggen te onderzoeken voor verschillende tijdsperiodes, geometrie en verkeersklassen. Figuur 4 laat de minimale wapening in een middenveld in de tijd zien voor een constant brugontwerp met glad betonstaal. Hieruit blijkt dat volgens de toegepaste methoden in het brugontwerp van 1930 tot 1970, dit in de periode 1950-1962 geleid heeft tot de laagste hoeveelheid toegepast glad betonstaal As (in cm2). Voor de tijdsperiode 1950-1962 zijn de unity checks voor het buigend moment in een middenveld (en bij de tussensteunpunten) groter dan 1,0, zie figuur 4. Verfijning in de herberekening is echter nog mogelijk, bijvoorbeeld met lineair elastische, eindig elementenmethoden [11]. De RBK v1.1 laat zien dat de dwarskrachtcapaciteit van bruggen, ontworpen met glad staal, niet afhankelijk is van de buigtrekwapening. De betondoorsnede bepaalt dus de dwarskrachtcapaciteit. De unity checks voor dwarskracht zijn in figuur 6 te zien. Opvallend is dat deze alle onder de 1,0 zijn. De toetsing met het decentraal belastingmodel laat unity checks zien voor het buigend moment in een middenveld van onder de 1,0, zie figuur 6. Tabel 3 geeft de toetsresultaten van de klasse B-bruggen met RE wapening, waar getoetst is volgens ’CC2 verbouw’ en met het decentraal belastingsmodel. Klasse A-bruggen met RE wapening zijn getoetst volgens ‘CC3 verbouw’ en met het decentraal belastingsmodel, zie tabel 4. Uit documentatie blijkt namelijk dat sommige
bruggen ontworpen zijn voor klasse A terwijl ze in een lokaal netwerk liggen. De resultaten voldoen aan de verwachting dat de buigend momentcapaciteit van deze bruggen hoger is dan voor de klasse B-bruggen.
DISCUSSIE/CONCLUSIE
De parametrische studie geeft een globaal inzicht in de huidige capaciteit van bestaande betonnen plaatbruggen, gebouwd in de periode 1930-1970 gewapend met glad betonstaal. De studie laat grote verschillen zien in de capaciteitsmarges in het constructief ontwerp in de periode 1930-1970. Het brugontwerp in de periode 1950-1962 heeft geleid tot laagste capaciteitsmarge volgens de toetsing met de huidige normen (NEN8700 serie [7] en de RBK v1.1 [9]). De focus in de huidige literatuur ligt hoofdzakelijk op de dwarskrachtbepaling van bestaande betonnen plaatbruggen in plaats van die op buigend moment. Echter, de Reverse Engineering-studie laat zien dat het
tegenovergestelde het geval is voor bruggen ontworpen voor betonsterkteklasse B45.
REFERENTIES
- Koninklijk Instituut van Ingenieurs, Gewapend Beton Voorschriften (GBV1912), Afdeling Bouw en Waterbouwkunde, 1912.
- Directie van Waterstaat, Voorschriften voor het ontwerpen van stalen bruggen (VOSB1933), Technical report, Ministerie van Waterstaat, 1933.
- NEN1991, Nationale bijlage bij NEN-EN1991-2+C1: Eurocode1: Belastingen op constructies–Deel2: Verkeersbelasting op bruggen. Normcommissie 351001 “Technische Grondslagen voor Bouw constructies”, 2011.
- Allaix, D., La Gasse, L., Steenbergen, R., en Vervuurt, A., Verkeersbelasting model voor wegverkeers- bruggen in het onderliggend wegennet zonder jaarontheffingen, Technical report, De Nederlandse Organisatie voor toegepast-natuurwetenschappelijk onderzoek (TNO). TNO-R10614, 2018.
- Mulder, R., Onderzoek gemeentelijke bruggen’, Bouwend Nederland p.1–15. Bouwend Nederland, de vereniging van bouw-en infra bedrijven, 2015.
- G. van Rossum, Python tutorial, Technical Report CS-R526, Centrum voor Wiskunde en Informatica (CWI), Amsterdam, 1995.
- NEN8700, Assessment of existing structures in case of reconstruction and disapproval -Basis Rules, Normcommissie 351001 “Technische Grondslagen voor Bouwconstructies”, 2011.
- NEN8701, Assessment of existing structures in case of reconstruction and disapproval-Actions, Normcommissie 351001 “Technische Grondslagen voor Bouwconstructies”, 2011.
- RWS en GPO, Richtlijnen Beoordeling Kunstwerken (RBK), Beoordeling van de constructieve veiligheid van een bestaand kunstwerk bij verbouw, gebruik en afkeur, Utrecht: RWS, GPO, 2013.
- Hofman, J. en van der Vlugt, B., ‘Berekening van balkrooster- en plaatbruggen’, Cement 8, Nr.19-20, 1956.
- De Boer, A., Lantsoght, E. O. L. en Van der Veen , C. Levels of Approximation for the shear assessment of reinforced concrete slab bridges, Structural Concrete, 18, 143-152, 2017.
|
Klasse B
1950 - 1962
|
Eurocode
(NEN8700 CC2 verbouw)
|
Decentraal
belastingsmodel
|
|
middenveld
|
1,0 - 1,30
|
0,85 - 0,95
|
|
middensteunpunt
|
0,90 - 1,15
|
0,75 - 0,90
|
|
dwarskracht
|
0,55 - 0,90
|
0,45 - 0,80
|
Tabel 3 Overzicht van unity checks volgens toetsing met de herberekeningsnormen van verkeerklasse B-bruggen uit de periode 1950-1962.
|
Klasse A
1950 - 1962
|
Eurocode
|
Decentraal
belastingsmodel
|
|
Middenveld
|
0,95 – 1,09
|
0,74 – 0,77
|
|
Middensteunpunt
|
0,85 – 0,97
|
0,60 – 0,80
|
|
Dwarskracht
|
0,60 – 1,04
|
0,40 – 0,85
|
Tabel 4 Overzicht van unity checks volgens toetsing met de herberekeningsnormen van verkeerklasse B-bruggen uit de periode 1950-1962.
Download hier het artikel in pdf-formaat 
|












